19+ disjoint vector spaces
For example Desargues theorem is self-dual in. A topological space X is called locally Euclidean if there is a non-negative integer n such that every point in X has a neighborhood which is homeomorphic to real n-space R n.
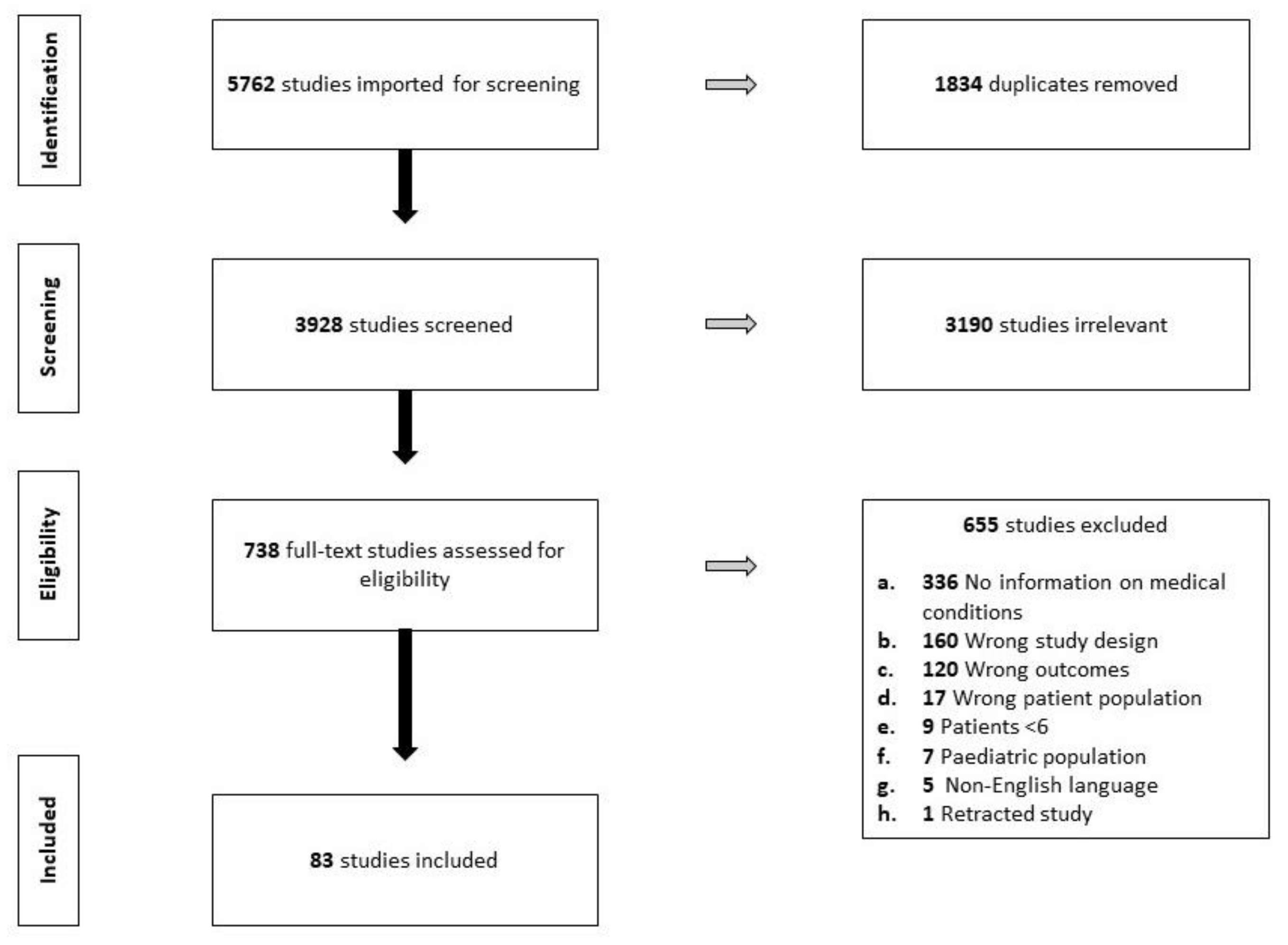
Ijerph Free Full Text Pre Existing Medical Conditions A Systematic Literature Review Of A Silent Contributor To Adult Drowning Html
Disjoint Tests whether geometries do not spatially intersect.
. Disjoint Tests whether geometries do not spatially intersect. Working with Mesh Data. It is unknown whether this is true or false even in the case of two variables.
Working with OGC ISO protocols. In fact by choosing a Hilbert basis E ie a maximal orthonormal subset of L 2 or any Hilbert space one sees that every Hilbert space is isometrically isomorphic to ℓ 2 E same E as above ie a Hilbert space of type ℓ 2. Let X be a topological space and A B be two subspaces whose interiors cover X.
Working with Vector Data. In geometry a line is an infinitely long object with no width depth or curvatureThus lines are one-dimensional objects though they may exist in two three or higher dimension spaces. Spaces and the Riesz representation theorem for bounded linear functionals on spaces of continuous functions.
This follows directly from the triangle inequality obeyed by the norm. Working with Mesh Data. In mathematical physics Minkowski space or Minkowski spacetime m ɪ ŋ ˈ k ɔː f s k i-ˈ k ɒ f- is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded.
Working with Vector Data. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal basisThe Haar sequence is now recognised as the first known wavelet basis and extensively used as a. Other than a few marked.
These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. A topological manifold is a locally Euclidean Hausdorff spaceIt is common to place additional requirements on topological manifolds. The representation theory of groups is a part of mathematics which examines how groups act on given structures.
There are other common definitions. This is a topological vector space because. The vector addition map.
They are all equivalent if X is a Hausdorff space or preregular. Books I through IV and VI of Euclids Elements dealt with two-dimensional geometry developing such notions as similarity of shapes the Pythagorean theorem Proposition 47 equality of angles and areas parallelism the sum of the angles in a triangle and the three cases in which triangles are equal have the same area among many other topics. It states that if a vector-valued polynomial function has a Jacobian determinant that is an invertible polynomial that is a nonzero constant then it has an inverse that is also a polynomial function.
But they are not equivalent in general. In particular many authors define them to be. HahnBanach dominated extension theorem for real linear functionals If.
Working with OGC ISO protocols. LLVM IR optionally allows the frontend to denote pointers in certain address spaces as non-integral via the datalayout string. Defined by is jointly continuous with respect to this topology.
The address space qualifier may be used in. We extract from these results a simple practical algorithm for the construction of a polynomial-reproducing spline space S r for r 0 k over any point configuration A which we present in Algorithm 1We apply here a few additional requirements to the process of 8 Theorem 210 and 8 Theorem 33In particular we assume that all the points lying on conv A are repeated k 1. All these topics can be found in the references.
That the space not exclude any limiting values of points. Basic versions for singular homology. Working with Vector Tiles.
It is disjoint from. For example the open interval 01 would not be compact because it excludes the. In mathematics the Haar wavelet is a sequence of rescaled square-shaped functions which together form a wavelet family or basis.
Hilbert spaces are central to many applications from quantum mechanics to stochastic calculusThe spaces L 2 and ℓ 2 are both Hilbert spaces. The word line may also refer to a line segment in everyday life which has two points to denote its ends. Every point of X has a compact.
Here the focus is in particular on operations of groups on vector spacesNevertheless groups acting on other groups or on sets are also considered. An element of the form is called the tensor product of v and wAn element of is a tensor and the tensor product of two vectors is sometimes called an elementary tensor or a decomposable. INF NaN and Denormalized Numbers.
Although initially developed by mathematician Hermann. The interiors of A and B need not be disjoint The MayerVietoris sequence in singular homology for the triad X A B is a long exact sequence relating the singular homology groups with coefficient group the integers Z of the spaces X A B and the. Array_mean Returns the mean of arithmetic values in an array.
Working with Vector Tiles. Every normed vector space has a natural topological structure. Working with Raster Data.
Descriptive set theory is the study of subsets of the real line and more generally subsets of Polish spacesIt begins with the study of pointclasses in the Borel hierarchy and extends to the study of more complex hierarchies such as the projective hierarchy and the Wadge hierarchyMany properties of Borel sets can be established in ZFC but proving these properties. In mathematics the concept of a measure is a generalization and formalization of geometrical measures length area volume and other common notions such as mass and probability of events. The norm induces a metric and the metric induces a topology.
Lines can be referred by two points that lay on it eg or by a single letter eg. For more details please refer to the section on permutation representations. Measures are foundational in probability theory.
Is a sublinear function which. Vector data types with two or more components such as char2. Laying out the maps.
In mathematics the tensor product of two vector spaces V and W over the same field is a vector space to which is associated a bilinear map that maps a pair to an element of denoted. Array_mean Returns the mean of arithmetic values in an array. Working with Raster Data.
If the dual of A is B then the dual of B is ASuch involutions sometimes have fixed points so that the dual of A is A itself. In mathematics more specifically in functional analysis a Banach space pronounced is a complete normed vector spaceThus a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well defined limit that is within the space. That is the integral representation may be target dependent or unstable not backed by a fixed integer.
Non-integral pointer types represent pointers that have an unspecified bitwise representation. OpenCL implements disjoint named address spaces with the spelling __global __local __constant and __private. In mathematics specifically general topology compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no holes or missing endpoints ie.
In mathematics a duality translates concepts theorems or mathematical structures into other concepts theorems or structures in a one-to-one fashion often but not always by means of an involution operation. Is a sublinear function such as a norm or seminorm for example defined on a real vector space then any linear functional defined on a vector subspace of that is dominated above by has at least one linear extension to all of that is also dominated above by. In mathematics a differentiable manifold also differential manifold is a type of manifold that is locally similar enough to a vector space to allow one to apply calculusAny manifold can be described by a collection of charts One may then apply ideas from calculus while working within the individual charts since each chart lies within a vector space to which the usual rules of.
Laying out the maps. Let X be a topological spaceMost commonly X is called locally compact if every point x of X has a compact neighbourhood ie there exists an open set U and a compact set K such that. And other examples of measures including k-dimensional Hausdorff measure in Rn Wiener measure and Brownian mo-tion and Haar measure on topological groups.

Final Approach How Airports Can Prepare For Advanced Air Mobility Mckinsey

Topological Vector Space Wikipedia
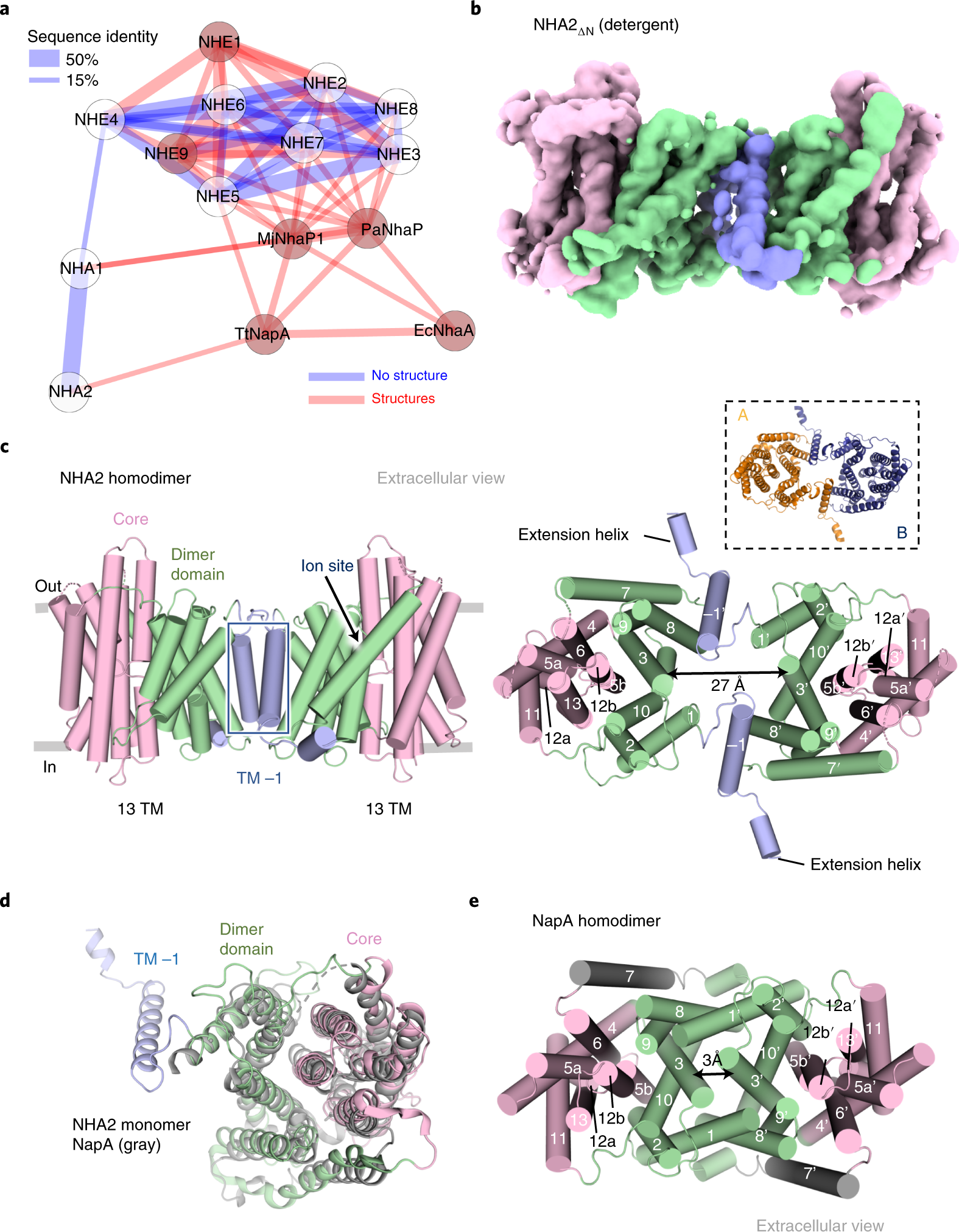
Structure Mechanism And Lipid Mediated Remodeling Of The Mammalian Na H Exchanger Nha2 Nature Structural Molecular Biology
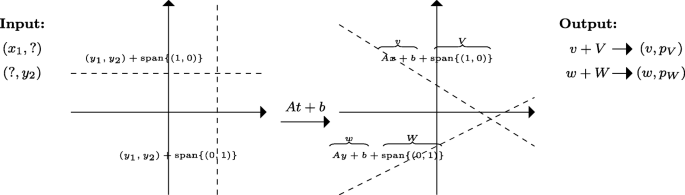
Pointed Subspace Approach To Incomplete Data Springerlink

24 Intersections And Sums Of Subspaces Youtube
Pre Processing Methods In Chest X Ray Image Classification Plos One

Masserstein Robust Linear Deconvolution By Optimal Transport Biorxiv

Kgv College
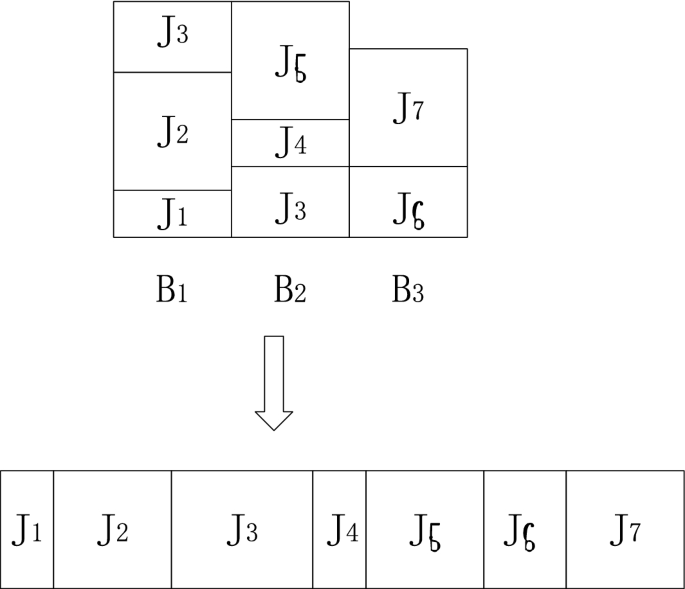
Single Machine Batch Scheduling With Two Non Disjoint Agents And Splitable Jobs Springerlink
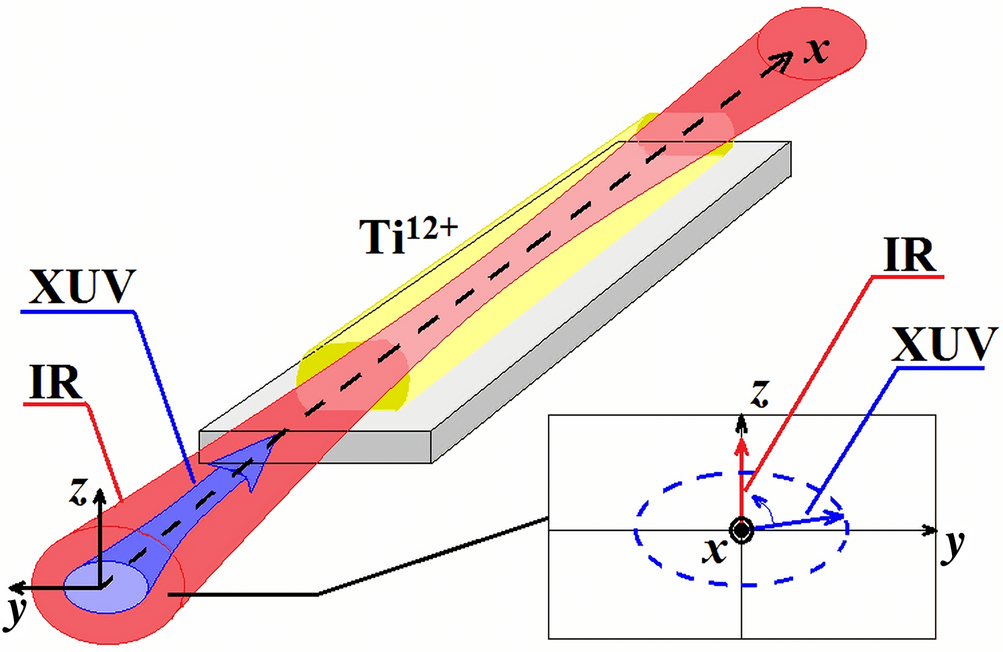
Amplification Of Elliptically Polarized Sub Femtosecond Pulses In Neon Like X Ray Laser Modulated By An Ir Field Scientific Reports

Global Impact Of The First Year Of Covid 19 Vaccination A Mathematical Modelling Study The Lancet Infectious Diseases
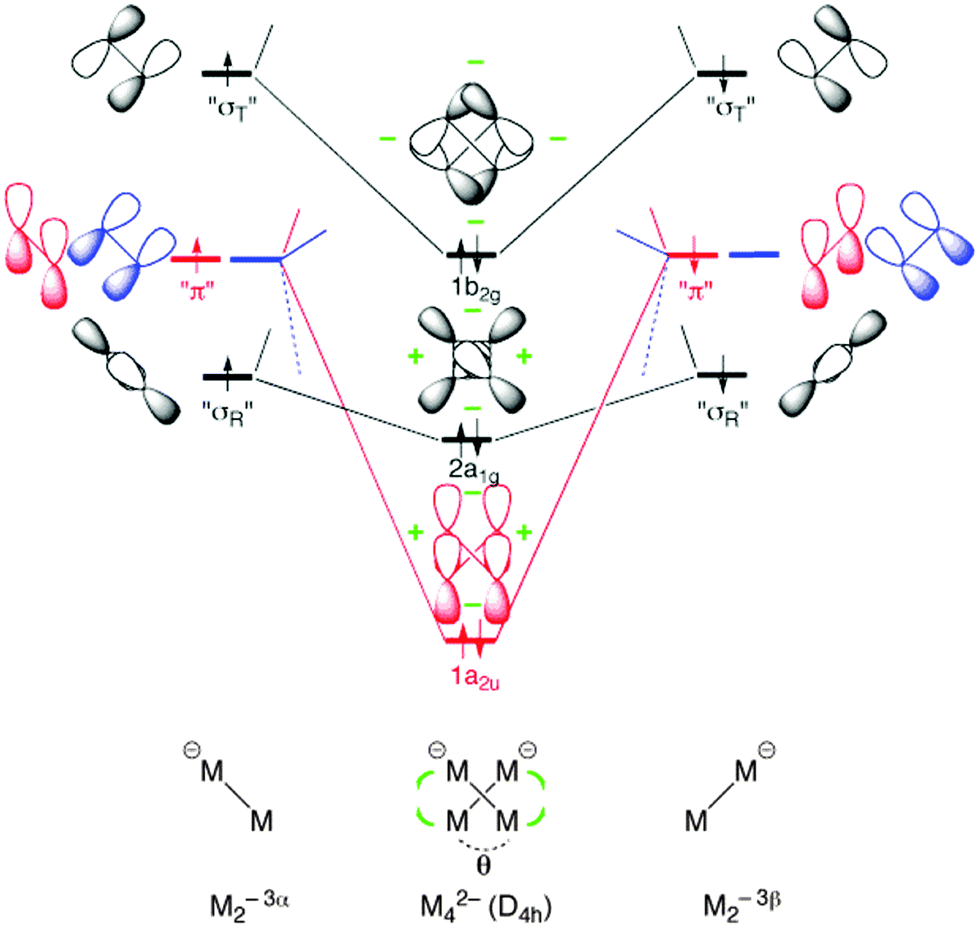
Quantifying Aromaticity With Electron Delocalisation Measures Chemical Society Reviews Rsc Publishing Doi 10 1039 C5cs00066a

Multiple Roles Of Sars Cov 2 N Protein Facilitated By Proteoform Specific Interactions With Rna Host Proteins And Convalescent Antibodies Jacs Au

Covid 19 Stay Up To Date With The Latest On Unops Support To Unops
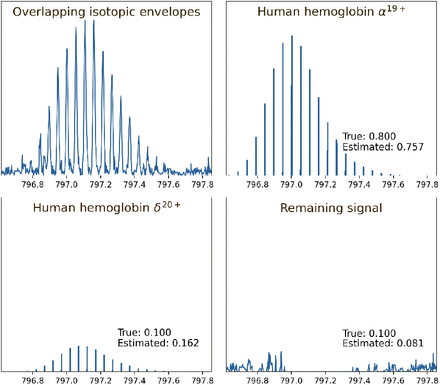
Masserstein Robust Linear Deconvolution By Optimal Transport Biorxiv

Your Future Starts Here Coleg Cambria

Vector Space Wikipedia